When creating an experiment, we provide recommended running times and sample sizes based on the parameters you choose. These values serve as estimates for how long to run the experiment. You can end the experiment early if you observe a significant effect.
For trend experiments, we use Lehr's equation to determine sample sizes.
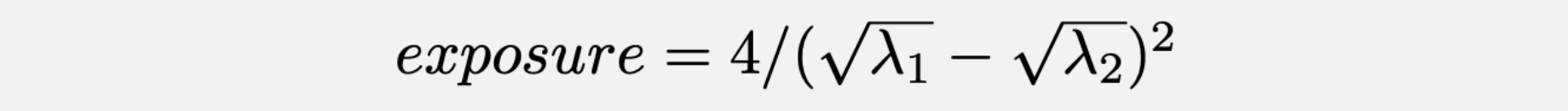

Here, lambda1 (λ1) represents the baseline count data from the past two weeks, and lambda2 (λ2) is calculated as baseline count + MDE * (baseline count). The MDE (minimum detectable effect) is the minimum acceptable improvement you select in the UI.
For funnel experiments, we use the general sample size determination formula, with 80% power and 5% significance level. The formula is as follows:


These values serve as estimates for how long to run the experiment. It's possible to conclude experiments early if you observe a significant effect.
Minimum detectable effect (MDE)
When setting up an experiment, the minimum detectable effect (MDE) is a required parameter for estimating sample size and running time. The MDE represents the smallest change or difference that you want to be able to detect in your experiment. Essentially, it's the minimum improvement you would consider significant.
To make things easier, we provide an estimated MDE value by default. This enables you to create experiments quickly without getting stuck on this step. However, we encourage you to review and adjust this value based on your specific goals.
It's important to understand that the recommended sample size decreases as the MDE increases. In other words, if you are looking for a smaller improvement, you'll need a larger sample size to detect it. This is because smaller effects are harder to identify and require more data to ensure the results are statistically significant.
Conversely, if you're looking for a larger improvement, you won't need as many samples because the effect is easier to spot. This relationship helps ensure that your experiment is sensitive enough to detect the changes you're interested in.